First-order kinetics in a CMBR

Environmental engineering

Author

Marco A. Alsina

Published

January 6, 2026

Problem statement

Lets consider 3 continuously mixed batch reactors (CMBRs) where a substance with initial concentration \(C_0\) decays with a first-order rate constant \(k_1\). The parameters for each reactor are listed below:

  • CMBR 1: \(C_0\) = 10 mg/L , \(k_1\) = 0.1 s\(^{-1}\)
  • CMBR 2: \(C_0\) = 5 mg/L , \(k_1\) = 0.1 s\(^{-1}\)
  • CMBR 3: \(C_0\) = 2 mg/L , \(k_1\) = 0.1 s\(^{-1}\)
  1. Plot the concentration in each reactor as a function of time.
  2. ¿What is the concentration of the substance in each reactor after 10 sec?

Solution

For a CMBR of constant volume \(V\), the concentration of a substance \(C\) that decays with a first-order rate constant \(k_1\) can be modeled as follows:

\[ \dfrac{dC}{dt}V = k_1 C V \tag{1}\]

Assuming that at time \(t=0\) the concentration of substance is \(C_0\), the previous ordinary differential equation (ODE) has the following analytical solution:

\[ C(t) = C_o e^{-k_1t} \tag{2}\]

Note that, in this case, the concentration in the CMBR is independent of the reactor volume. Lets implement this last equation numerically through a function:

from numpy import linspace, exp
import matplotlib.pyplot as plt

def conc(C0, k1, time):
    '''Concentration in a CMBR with first-order decay
    '''
    return C0 * exp(-k1 * time)

Note that our function receives the initial concentration C0, the first-order decay rate constant k1, and the time array. We can use the same function to model the 3 CMBRs.

Plot of concentration

fig, ax = plt.subplots(figsize=(3,3)) # figure size

time    = linspace(0, 20) # time in sec
k1      = [0.1, 0.1, 0.1] # fist-order decay rate constant (1/s)
C0      = [ 10,  5,  2]   # initial concentrations (mg/L)

for i, k in enumerate(k1):
    Ct = conc(C0[i], k, time)
    col = str(i*0.25)
    ax.plot(time, Ct, color=col, label="$C_0$ = %s mg/L" % C0[i])

ax.axvline(10, color='k', ls=':') 
ax.set_xlabel("time [s]")
ax.set_ylabel("concentration [mg/L]")
ax.legend(edgecolor='k')
ax.grid()
plt.show()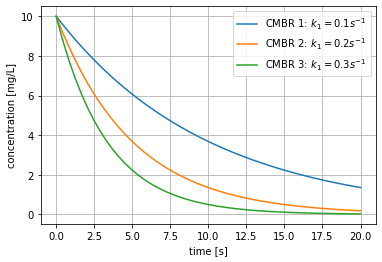

As expected from Equation 2, the concentration of each CMBR decays exponentially as a function of time. We additionally plot a vertical line at \(t=10\) s to visually inspect the concentration at this time.

From Equation 2 we also note that \(1/k_1\) corresponds to the time required to reduce the concentration in the reactor to \(C_0/e\), which is roughly \(\sim\) 37% of the original concentration.

Concentration after 10 sec

We can use our function considering 10 sec as the input time to compute the concentration of the substance.

t_eval = 10 # sec

for i, k in enumerate(k1):
    conc_t = conc(C0[i], k, t_eval)
    print ("CMBR %i: C(t=%s[s]): %1.3f [mg/L]" % (i+1, t_eval, conc_t) )
CMBR 1: C(t=10[s]): 3.679 [mg/L]
CMBR 2: C(t=10[s]): 1.839 [mg/L]
CMBR 3: C(t=10[s]): 0.736 [mg/L]

Follow up questions

  1. Show that the time it takes a CMBR to reach half of the initial concentration \(t_{1/2} = -\ln(0.5)/k_1\).
  2. Verify that after a time equal to \(1/k_1\) the concentration in the CMBR is \(C_0/e\).
  3. How much time is required for the concentration to be exactly zero in each reactor?