NaCl diffusion from a point source
Water quality
Problem statement
Consider the diffusion of NaCl inside a pipe that suddently receives an input mass \(M_0\). Assume that the diffusion coefficient of NaCl in water is 1.61x10-5 cm2/s, the input mass \(M_0\) is 0.2 mg NaCl, the inner surface area \(A\) of the pipe is 100 cm\(^2\), and the NaCl concentration inside the pipe is 0 mg/L.
- Plot the concentration of NaCl inside around the point source of the pipe after 30 minutes.
- Compute the concentration of NaCl at the point source after 30 minutes.
Solution
The partial differential equation (PDE) that describes the concentration \(C\) of a substance that is transported by diffusion (\(D\)) in a 1-D domain (\(x\)) is as follows:
\[ \begin{equation} \left\{ \begin{aligned} &\frac{\partial{C}}{\partial{t}} = D\frac{\partial^2{C}}{\partial^2{x}} \qquad 0 \le x < \infty, t > 0 \\ \\ &C(x)|_{t=0} = g(x) \qquad 0 \le x < \infty \end{aligned} \right. \end{equation} \tag{1}\]
This PDE can be computed for restricted cases. For the case of a point source of mass \(M_0\) located at \(x_0\) of a pipe with inner surface area \(A\), the PDE has the following analytical solution:
\[ C(x,t) = \frac{M_0}{2A\sqrt{\pi D t}} \cdot \text{exp} \left( \frac{-(x-x_0)^2}{4Dt} \right) \tag{2}\]
Lets implement this equation numerically through a function:
Our function receives the initial input mass M0, the diffusion coefficient D, the inner surface area of the pipe A, the x domain of the pipe, the location x0 of the point source mass, and the time.
Note that we are passing an array of values for \(x\), in order to compute the substance concentration at the domain for a given time.
Plot of NaCl concentration
To compute the concentration of NaCl inside the pipe we are arbitrarily considering a pipe section of 1 cm length, discretized in 41 points, with the input source at the center of the section (\(x_0\)=0.5). Note that we need to provide the time in seconds and the length in cm, in order to keep consistency with the units of the diffusion constant D. In addition we divide the input mass by 10\(^3\) to convert concentration from mg/cm3 to mg/L.
Finally, we will use a matrix array named ctx to store the concentration of NaCl inside the pipe at the different time intervals, to track the evolution of concentration. Thus our array will have a shape of 3 rows and 41 columns.
from numpy import linspace, vstack, empty
from matplotlib import cm
import matplotlib.pyplot as plt
m0 = 0.2 # mass in mg
a = 100 # surface area in cm2
x0 = 0.5 # point source location in cm
D = 1.61e-5 # diffusion coefficient NaCl in cm^2/s
mtime = [10, 20, 30] # time in mins
stime = [t*60 for t in mtime] # time in secs
x = linspace(0,1,41) # distance in cm
ctx = empty((len(mtime), len(x))) # container of concentrations
# concentration as a function of time
for i, t in enumerate(stime):
ctx[i,:] = conc(m0, D, a, x, x0, t)*1e3
# plot results
fig, ax = plt.subplots(figsize=(6,6))
grays = cm.get_cmap('bone_r', len(mtime)+1)
ax.set_prop_cycle(color = [grays(i+1) for i in range(len(mtime))])
for i, t in enumerate(mtime):
ax.plot(x, ctx[i,:], label='%i mins'%(t) )
# axes decorators
ax.set_xlabel('distance [cm]')
ax.set_ylabel('NaCl [mg/L]')
ax.set_title('NaCl diffusion in water')
ax.legend(edgecolor='k')
plt.show()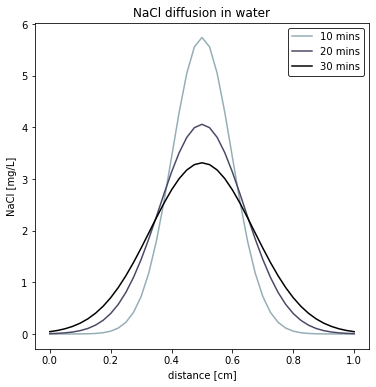
NaCl concentration at the point source
Since we stored our results in the ctx array, the concentration of NaCl at the point source corresponds the middle column of the array. Thus we can slice the array and print the values to obtain the values:
NaCl concentration at the point source:
10 minutes: 5.74 mg/L
20 minutes: 4.06 mg/L
30 minutes: 3.31 mg/LFollow up
- Compute the concentration of NaCl at the source point after 60 minutes.
- Compute the concentration of NaCl at the domain boundaries after 60 minutes.
- Expand the function to compute the total mass of NaCl in the pipe section.
- Modify Equation 2 to locate the point source at \(x\)=0, assuming that no diffusion occurs for \(x<0\). Check the total mass in the pipe section.